11-6-12
Пусть an – первая (старшая) цифра в десятичном разложении
n2 при n =1,2,3,... (a1 = 1, a2 = 4, a3 = 9, a4 = 1, a5 = 2,…). Докажите, что
данная последовательность не является периодической.
- Решение
Решение
Пусть b – произвольная цифра от 1 до 9 и k – любое натуральное
число. Тогда для всех номеров n , удовлетворяющих неравенству
последовательность an постоянна и совпадает с b , поскольку
Осталось заметить, что при росте k длина отрезка
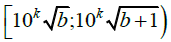
неограниченно возрастает
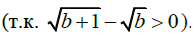
.
Следовательно, в нашей последовательности найдутся сколь угодно
много подряд идущих единиц, двоек, …, девяток. Поэтому она не может
быть периодической.
- Ответ
Ответ
Что и требовалось доказать.