Решение
Обозначим
^{2018}})
и
^{2017}})
. Пользуясь формулой для суммы членов геометрической прогрессии, находим:
^{2018} }}{{9^{2018} }}})
,
^{2017} }}{{9^{2017} }}})
. Обозначим
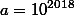
. Оценим разность:
^{2018} - 9 \cdot \left( {10a - 1} \right)^{2017} } \right) = 9^{ - 2018} \cdot C})
. Здесь
^{2018} - 9 \cdot \left( {10a - 1} \right)^{2017}})
. Определим знак
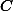
. Увеличим вычитаемое, заменив
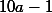
на
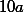
:
^{2018} - 9 \cdot \left( {10a} \right)^{2017} = \left( {a - 1} \right)^{2018} - 0,9 \cdot a^{2018}})
. Знак последнего выражения, очевидно, совпадает со знаком разности
^{2018} - 0,9})
. Заметим, что
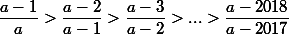
. Следовательно,
^{2018} > \frac{{a - 1}}{a} \cdot \frac{{a - 2}}{{a - 1}} \cdot \frac{{a - 3}}{{a - 2}} \cdot ... \cdot \frac{{a - 2018}}{{a - 2017}} = \frac{{a - 2018}}{a}
})
. Далее,
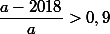
, так как
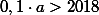
. Следовательно, разность
^{2018} - 0,9})
, а вместе с ней и
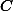
, положительны. Следовательно, первое число больше второго.