Что на что делится

Про натуральные числа известно следующее:
• делится на с;
• делится на a;
• делится на b.
Докажите, что делится на произведение

• Подсказка

Подсказка

Рассмотреть простые делители чисел a, b, c.
• Решение

Решение

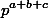
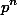
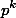
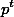
Пусть p – простой делитель числа a. Тогда из 2-го условия следует, что b делится на p, а из 3-го – что c делится на p. Следовательно, делится на . Пусть n,k,t – наибольшие натуральные числа такие, что a делится на , b делится на , c делится на . Значит, в каноническое разложение произведения abc простое число p входит в степени n+k+t. Но, очевидно, a>n, b>k, c>t. Поэтому a+b+c > n+k+t и, следовательно, число делится на . 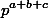Рассмотрев подобным образом остальные простые делители чисел a,b,c, получим требуемое утверждение.
• Ответ

Ответ

См. решение.