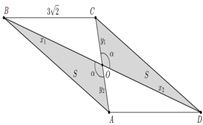
Докажем, что четырехугольник ABCD – параллелограмм. Пусть
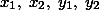
– отрезки, на которые диагонали делятся их точкой пересечения. Обозначим угол между диагоналями через α.
По условию площади треугольников ABO и CDO равны, то есть

. Отсюда
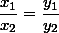
, и, следовательно, треугольники BOC и AOD подобны по первому признаку подобия: две стороны (
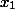
и
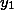
) треугольника BOC пропорциональны двум сторонам (
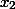
и
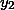
) треугольника AOD, а углы, образованные этими сторонами (
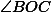
и
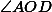
), равны. Пусть
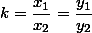
– коэффициент подобия треугольников BOC и AOD. Обозначим через S площади треугольников ABO и CDO (по условию
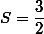
). Тогда

и

. В итоге, площадь четырехугольника ABCD может быть представлена в виде:
. })
Известно, что для k>0 минимальное значение выражения
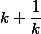
достигается при k=1. Значит,

, то есть диагонали четырехугольника точкой пересечения делятся пополам, поэтому ABCD – параллелограмм. Его площадь

Для нахождения синуса угла между диагоналями воспользуемся тем, что площадь четырехугольника равна половине произведения диагоналей на синус угла между ними:
 })
Чтобы найти длины диагоналей, вычислим сторону CD, записав формулу для площади параллелограмма