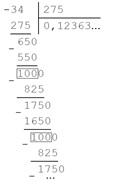Решение
Рассмотрим пример. Переведем обыкновенную дробь
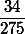
в десятичную. Для этого выполним деление уголком (рис.).
В результате найдем
. })
Получена непериодическая часть 123 и период 63. Обсудим, почему непериодическая часть здесь возникла, и покажем, что у дроби
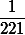
ее нет. Дело в том, что в десятичной записи дроби
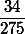
цифра 3 появляется всякий раз, когда при очередном делении на 275 получается остаток 100. Мы видим (и это ключевой момент!), что здесь один и тот же остаток 100 дают
различные числа: 650 и 1750. Откуда, в свою очередь, взялись эти 650 и 1750? Число 650 получилось дописыванием нуля к числу

(остатку от деления на 275 числа 340). То есть

Аналогично,

где

Числа 650 и 1750 дают одинаковые остатки при делении на 275 из-за того, что их разность на 275 делится нацело:
\; \vdots \;275. })
Такое возможно только потому, что числа 10 и 275 не взаимно просты. Теперь понятно, почему у дроби
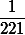
непериодической части не будет: если
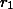
и
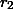
– это различные остатки от деления на 221, то произведение
 })
на 221 нацело не делится (число 221, в отличие от 275, взаимно просто с 10 – основанием системы счисления, поэтому непериодической части нет). Итак, десятичная запись дроби
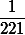
имеет вид
. })
Найдем n. Обозначим
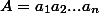
. Тогда

. По формуле для суммы бесконечно убывающей геометрической прогрессии

. Отсюда

. Поскольку A – натуральное число, требуется найти (наименьшее) натуральное n, при котором число
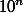
дает остаток 1 при делении на 221. Заметим, что 221=13∙17. Вообще, целое число B (у нас
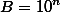
) при делении на 221 дает остаток 1 в том и только том случае, когда B при делении и на 13, и на 17 также дает остаток 1. Необходимость очевидна. Достаточность: если

и

, то

, а значит число
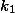
делится на 17, то есть

. Поэтому

, и при делении на 221 действительно получается остаток 1. Найдем теперь такие n, что число
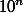
дает остаток 1 при делении на 13. Рассмотрим последовательность

. Заменим ее члены остатками от деления на 13. Получится вот что:

. Каждый последующий член однозначно определяется предыдущим. Значит,
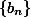
– периодическая последовательность, в которой каждый шестой член равен 1. То же проделаем для 17. Там единице будет равен каждый 16-й член. Таким образом, остаток 1 при делении и на 13, и на 17 получится при n=НОК(6,16)=48.
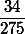 в десятичную. Для этого выполним деление уголком (рис.).
в десятичную. Для этого выполним деление уголком (рис.).