Морской бой

Аня с Борей играют в «морской бой» по следующим правилам: на окружности выбираются 29 различных точек, пронумерованных по часовой стрелке натуральными числами от 1 до 29. Аня рисует корабль – произвольный треугольник с вершинами в этих точках. Будем называть «выстрелом» выбор двух различных натуральных чисел k и m от 1 до 29. Если отрезок с концами в точках с номерами k и m имеет с треугольником Ани хотя бы одну общую точку, то корабль считается «раненым». Боря производит «залп» – несколько выстрелов одновременно.  Аня нарисовала корабль и показала его Боре. И тут они заметили, что любой «залп» из K различных выстрелов обязательно ранит корабль Ани. Укажите какое-нибудь расположение корабля Ани, при котором значение К будет минимальным.

• Подсказка

Подсказка

Ввести две переменные (для количества точек на дугах), подсчитать количество "безопасных" выстрелов и определить значения переменных, при которых это количество минимально.
• Решение

Решение

Вершины треугольника Ани делят окружность на три дуги. Пусть x,y и 26-x-y – количество точек на этих дугах, не считая вершины самого треугольника. Чтобы «выстрел» с концами в точках k и m не задел корабль, надо чтобы обе эти точки лежали на одной из дуг. Выбрать две различные точки на дуге, содержащей x точек, можно, очевидно, способами. То же и для остальных дуг. Значит число N «безопасных» выстрелов равно сумме . Тогда следующий выстрел уже обязательно «ранит» корабль, поэтому K=N+1. Итак, требуется найти такие целые неотрицательные числа x,y, удовлетворяющие условию x+y≤26, при которых значение N минимально. Запишем выражение для N в развернутом виде: Раскрыв скобки и приведя подобные слагаемые, получим

  

При каждом фиксированном y от 0 до 26 будем искать такое значение x, удовлетворяющее неравенству

  

при котором значение N минимально. Если y фиксирован, то правая часть (1) принимает минимальное значение при

  

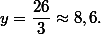
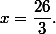
(вершина параболы, принадлежащая промежутку (2)). Это минимальное значение равно Оно, в свою очередь, минимально при Из (3) тогда находим Cреди точек с целыми координатами (8,8),(8,9),(9,8),(9,9) – ближайших целочисленных соседей точки минимума – выбираем ту, которой соответствует наименьшее значение N. Это точки (8,9),(9,8),(9,9). Для них N=100.
• Ответ

Ответ

Корабль следует расположить так, чтобы на трех дугах, на которые вершины корабля разбивают окружность, располагалось по 8, 9 и 9 точек (не считая вершины самого корабля).