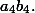Решение
Докажем, что
Умножим уравнение (a) исходной системы
на
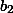
и вычтем из него уравнение (b), умноженное на
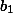
. В результате получим
Здесь

. Аналогично, из (c) и (d) находим, что
Заметим, что

, так как в противном случае из (3) следовало бы, что
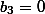
, а значит, и

, что противоречит условию задачи. Остается выразить
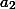
и
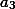
из (2) и (3) и подставить полученные выражения в (1). Справедливость соотношения (1) будет тем самым доказана. Далее из уравнения (d) и равенства (1) следует, что

Комментарий.
Система уравнений в задаче – это покомпонентная запись матричного равенства:
 })
,
где
 })
и
. })
Хорошо известно, что если произведение двух матриц равно единичной, то такие матрицы коммутируют, а значит система уравнений в задаче останется справедливой, если в ней все
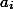
заменить на
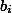
и наоборот. Из этого наблюдения равенство (1) следует немедленно.
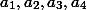 и
и 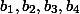 удовлетворяют соотношениям
удовлетворяют соотношениям Найдите
Найдите