Неизвестные степени
Решите уравнение- Подсказка
- Решение
- а) Пусть n=1. Тогда t=1. С учетом (2) и (4) находим решение исходного уравнения: x=1, y=2, t=1;
- б) Пусть n>1. Тогда левая часть (5) кратна 4. Если t нечетно, то правая часть (5) на 4 не делится. Значит, t=2m, где m - целое неотрицательное. Из (5) следует, что
Значит, числа
и
являются степенями двойки. Заметим также, что на числовой оси эти числа находятся друг от друга на расстоянии 2. Такое возможно, только если
и
Отсюда m=1 и тогда t=2, n=3. Подставляя найденные значения в (2) и (4), получаем решение x=2, y=5, t=2.
- Ответ
Подсказка
Рассмотреть отдельно случаи, когда x и y одинаковы и различны. Каждый случай разбить на две ветви: положительное (неотрицательное) t и неположительное (отрицательное) t.Решение
Пусть сначала x=y. Исходное уравнение в этом случае примет вид:
Если t>0, то правая часть (1) кратна трем, а левая –нет. Значит,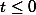 
. Если же предположить, что t<0, то, переписав (1) в виде 
, вновь придем к противоречию: кратное трем число 
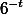не может быть никакой степенью двойки. Поэтому t=0 и x=y=-1.
Пусть теперь числа x и y различны. Можно считать, что x < y. Положим:
где n - натуральное. Исходное уравнение запишется в виде
Заметим, что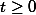 
. Действительно, из (3) следует, что  = 2^{t - x}. })
Если t < 0, то левая часть последнего равенства делится на 3, а правая – нет. Значит, 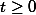. Но тогда и 
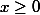(иначе, согласно (3), дробное число равнялось бы целому). Число 2 входит в канонические разложения на простые множители левой и правой частей (3) в одной и той же степени, поэтому
Сократив обе части (3) на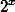 
и перенеся 1 в другую часть, получим
Решим уравнение (5), предполагая n натуральным, а t – неотрицательным целым.