Решение
Каждое 100-значное натуральное число может быть получено дописыванием двух цифр справа к 98-значному числу. Пусть x – некоторое 98-значное число. Посмотрим, какие справа две цифры (каждая из которых равна 1 или 2) нужно к числу x приписать, чтобы получившееся 100-значное число делилось на 3. Воспользуемся тем, что остаток от деления натурального числа на 3 равен остатку от деления на 3 суммы его цифр. Пусть наше число x при делении на 3 дает остаток m. Тогда:
а) если m=0, то припишем 12 или 21;
б) если m=1, то припишем 11;
в) если m=2, то припишем 22.
Таким образом, из каждого 98-значного числа, кратного 3, можно получить два кратных трем 100-значных числа. Каждое не кратное трем 98-значное число порождает только одно кратное трем 100-значное число. Всего 98-значных чисел
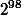
. Пусть среди них
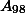
чисел кратно трем. (Далее символом
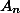
будем обозначать количество n-значных чисел, кратных 3.) Тогда количество кратных трем 100-значных чисел может быть найдено по формуле
 = 2^{98} + A_{98} })
.
Верны, таким образом, следующие соотношения:
...
Сложив эти равенства (величины
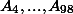
при этом сокращаются), получим

Остается просуммировать геометрическую прогрессию и заметить, что
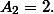
Тогда
