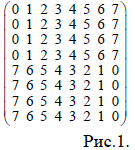
Решение
Пронумеруем линии клеток доски числами от 1 до 8 сверху вниз. На
первой линии позицию ладьи можно выбрать 8 способами. Например,
выбрали первую клетку с числом 0. На второй линии остаются 7 вариантов
выбора. Шесть из них (клетки со второй по седьмую) обладают тем
свойством, что под ними в нижней половине доски стоят числа,
отличающиеся от числа, занимаемого первой ладьей (в нашем случае – от
числа 0), а одна клетка (последняя, с числом 7), такова, что под ней в нижней
половине стоит число, занятое первой ладьей (в нашем случае – 0).
Рассмотрим первую группу из 6 вариантов выбора и сделаем
произвольный выбор (например, вторая клетка с числом 1). После такого
выбора получается, что в нижней половине доски запрещен выбор позиций с
двумя различными числами (в нашем случае 7 и 6). Поэтому позиции с этими
числами нужно выбрать в верхней половине доски, а таких вариантов ровно
2 (в нашем случае 7 и 8 клетки в линиях 3 и 4). После этого выбора в нижней
половине доски останутся 4 столбца с различными числами по столбцам. Т.е.
в нижней половине имеется 4! = 24 варианта выбора. Всего, таким образом,
получается 8х6х2х24 варианта.
Рассмотрим вариант выбора позиции во второй линии, когда под
выбранной клеткой в нижней половине доски стоит число, выбранное на
первой линии (в нашем случае последняя клетка с числом 7). После такого
выбора в третьей линии имеется 6 вариантов, приводящих к единственному
варианту в четвертой линии. После выбора вариантов в верхней половине
доски, в нижней опять остаются 4 свободных столбца с четырьмя
различными числами, т.е. 24 варианта. Всего, таким образом, получается
8х1х6х24 варианта.