Архив задач

На перепутье дорог (часть 2)

Пусть выполнены условия задачи "На перепутье дорог"
Путешественник выехал из некоторого города A, избрав себе следующий маршрут движения: из города A он выезжает по дороге с номером 1, из следующего города – по дороге с номером 2, затем с номером 3, далее – снова по дорогам с номерами 1, 2, 3, 1, 2 …. Докажите, что при таком маршруте движения путешественник обязательно вернется в город A.

  • Подсказка

    • Подсказка

    Описать движение путешественника последовательностью пар (город, дорога). Воспользоваться методом от противного.
  • Решение

    • Решение

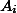
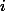
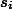
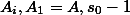
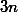
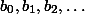
    Опишем маршрут движения путешественника последовательностью {b_i=(A_i,s_i), i=1,2,3,\ldots} где {A_i} - город, посещенный на {i} - ом шаге, {s_i} - номер дороги – выезда из города {A_i,A_1=A,s_0-1} . Количество всевозможных пар {b_i=(A_i,s_i)} равно {3n} , следовательно, на маршруте движения {b_0,b_1,b_2,\ldots} начнутся повторения.
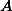
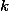
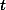
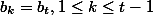
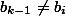
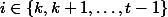
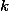
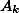
          Предположим, что в город {A} путешественник не вернется. Тогда найдутся натуральные числа {k} и {t} такие, что выполняются условия: {b_k=b_t, 1\le k \le t-1} и {b_{k-1}\ne b_i} , при всех {i\in \{k,k+1,\ldots,t-1 \}} (первый повтор членов последовательности {b_i=(A_i,s_i), i=1,2,3,\ldots} произошел на шаге с номером {k} ). 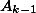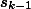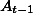Но тогда в город {A_k} путешественник попадает вначале из города {A_{k-1}} по дороге с номером {s_{k-1}} , а затем из города {A_{t-1}} по дороге с номером {s_{t-1}} . 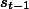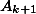При этом дальнейший маршрут движения в город {A_{k+1}} одинаковый. 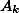Тогда ввиду однозначности маршрута, номера дороги, по которым попадаем в город {A_k} , совпадают. 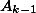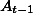Так как в каждый город ведут дороги с различными номерами, то города {A_{k-1}} и {A_{t-1}} совпадают. 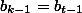Но тогда {b_{k-1}=b_{t-1}} . Получили противоречие. Следовательно, наше предположение не верно. А значит, утверждение доказано.
         
         
  • Ответ

    • Ответ

    см. решение