2.9.2006

• Подсказка

Подсказка

Задача решается методом перебора, но поскольку чисел различных семь, то простой перебор оказывается очень громоздким. Поэтому путем вычисления суммы по всем граням указанной фигуры и сопоставлением ее с суммой всех указанных чисел, следует перебрать все возможные варианты числа, находящегося в центральной вершине. Для каждого выбора такого числа проанализировать возможные варианты для чисел в других вершинах.
• Решение

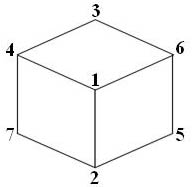
Решение

Обозначим число в центральной вершине . Элементы, соединенные с ним одним ребром, обозначим соответственно . Остальные числа будут расставлены в соответствии с условием задачи.

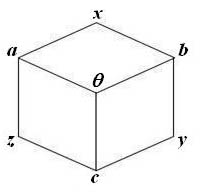
Поскольку по условию сумма по каждой грани должна равняться 14, то можем получить следующие уравнения для семи введенных переменных





Складывая все уравнения, получим





Рассмотрим возможные варианты значений . По условию .
1) Если , то из уравнения (*) получим





Поскольку все числа различны, то среди переменных нет числа 7. А поскольку сумма , то





Т.е. , что невозможно по условию, т.к. среди чисел от 1 до 7 нет трех различных, дающих в сумме 0.
2) Если , то из уравнения (*) получим





Поскольку все числа различны, то среди переменных нет числа 6. А поскольку сумма , то





Т.е. , что невозможно по условию.
3) Если , то из уравнения (*) получим





Поскольку все числа различны, то среди переменных нет числа 5. А поскольку сумма , то





Т.е. , что невозможно по условию.
4) Если , то из уравнения (*) получим





Поскольку все числа различны, то среди переменных нет числа 4. А поскольку сумма , то





Т.е. , что выполнено, если . Значит, возможно 6 вариантов, при которых 4 находится в центральной вершине. Переменные вычисляются исходя из условия суммы чисел в вершинах каждой грани. Один из вариантов представлен на рисунке:


5) Если , то из уравнения (*) получим





Поскольку все числа различны, то среди переменных нет числа 3. А поскольку сумма , то





Т.е. , что выполнено, если . Но в данном случае одна из граней исходной фигуры будет содержать три вершины 1, 2, 3, значит, четвертая вершина будет равна , что противоречит условию.
6) Если , то из уравнения (*) получим





Поскольку все числа различны, то среди переменных нет числа 2. А поскольку сумма , то





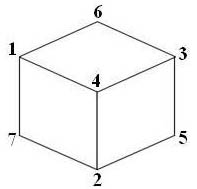
Т.е. , что выполнено, если или . В первом случае одна из граней исходной фигуры будет содержать три вершины 1, 2, 3, значит, четвертая вершина будет равна , что противоречит условию. Во втором случае возможно 6 вариантов расположения чисел. Один из них приведен на рисунке:


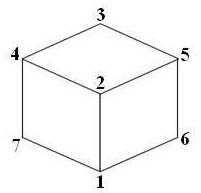
7) Если , то из уравнения (*) получим





Поскольку все числа различны, то среди переменных нет числа 1. А поскольку сумма , то





Т.е. , что выполнено, если или , или . В первом случае одна из граней исходной фигуры будет содержать три вершины 1, 4, 5, значит, четвертая вершина будет равна , что противоречит условию различия вершин. Во втором случае В третьем случае возможно 6 вариантов расположения чисел. Один из них приведен на рисунке:


• Ответ

Ответ