Архив задач

2.10-9.2005

В равнобочную трапецию с основаниями 3 и 5 вписана окружность, а в
нее, в свою очередь, вписана трапеция, подобная исходной. Найти
коэффициент подобия меньшей трапеции к большей.

  • Подсказка

    • Подсказка

    Заметить, что искомый коэффициент подобия равен отношению радиуса окружности, вписанной в исходную трапецию, к радиусу окружности, описанной около исходной трапеции.
  • Решение

    • Решение

    Исходя из условия задачи, коэффициент подобия равен отношению радиуса {r} окружности, вписанной в исходную трапецию, к радиусу {R} окружности, описанной около исходной трапеции. Поэтому найдем {R} и {r} .
    2.9_10.2005.jpg
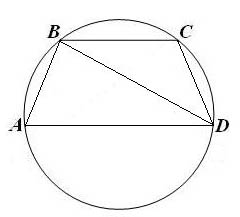
         Сделаем чертеж, на котором изобразим только исходную трапецию и окружность, описанную вокруг данной трапеции.
         Так как в трапецию можно вписать окружность, то сумма боковых сторон трапеции равна сумме оснований. Так как трапеция равнобочная, то боковые стороны трапеции равны {(3+5)/2=4} .
         Теперь легко вычислить высоту трапеции с помощью теоремы Пифагора:
    {h=\sqrt{4^2-\left(\frac{5-3}{2}\right)^2}=\sqrt{15}.}
    Радиус вписанной окружности, очевидно, равен половине высоты трапеции: {r=\sqrt{15}/2} .
         Радиус описанной окружности {R} найдем как радиус окружности, описанной около треугольника {ABD.}
         Синус угла {A} при основании трапеции равен {\sin A=\sqrt{15}/4} , отсюда находим {\cos A = 1/4} . По теореме косинусов для диагонали {BD} из треугольника {ABD} запишем
    { BD^2=AB^2+AD^2-2\cdot AB\cdot AD\cdot\cos }
    Поэтому диагональ трапеции {BD=\sqrt{31}} .
         Теперь по теореме синусов находим радиус окружности, описанной около треугольника {ABD.}
    { \frac{BD}{\sin A}=2R,\quad \frac{\sqrt{31}}{\sqrt{15}/4}=2R,\quad }
    Коэффициент подобия находим как отношение радиусов
    { \frac{r}{R}=\frac{\sqrt{15}}{2}\cdot\frac{\sqrt{15}}{2\sqrt{31}}=\frac{15}{4\sqrt{31}}. }
  • Ответ

    • Ответ

    {\frac{15}{4\sqrt{31}}} .