Решение
У натуральных чисел, кратных девяти, от 9 до 4950 надо подсчитать суммы цифр, а затем эти суммы сложить. Пусть
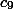
– количество чисел в этом диапазоне, у которых сумма цифр равна 9,
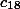
– количество чисел с суммой цифр 18,
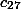
– количество чисел с суммой цифр 27.
Вычислим
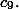
Будем все числа трактовать как четырехзначные: 9=0009, 18=0018, … Рассмотрим сначала числа вида

, т.е. те, у которых первая цифра ноль. Выясним, сколькими способами число 9 может быть представлено в виде суммы трех целых неотрицательных слагаемых:

Прибавим к обеим частям число 3:
 + (m_2 + 1) + (m_3 + 1).})
Получается, что надо найти количество способов представить число 12 в виде суммы трех натуральных слагаемых. Это количество равно
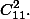
(Действительно, представим себе на числовой прямой числа 1,2,…,12. Между ними имеется 11 промежутков. Выбрав два промежутка, мы разобьем 12 на три ненулевых слагаемых.) Аналогично, имеется
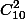
чисел с суммой цифр 9 вида
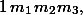
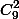
чисел
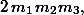
,
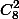
чисел
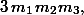
и, наконец,
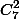
чисел вида
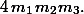
В итоге,

Затем нетрудно найти, что

и, следовательно,

Для получения ответа остается вычислить
