Оценка снизу для бинома Ньютона
Произведение положительных чисел a и b больше 1. Докажите, что для любого натурального n≥2 верно неравенство
^n > a^n + b^n + 2^n - 2})
.
- Подсказка
Подсказка
1. Рассмотреть, что представляет собой выражение
^n})
после раскрытия скобок.
2. Воспользоваться симметрией коэффициентов разложения.
3. Рассмотреть случай a=b=1.
4. Воспользоваться неравенством Коши.
- Решение
Решение
^n = a^n + t_{n - 1} a^{n - 1} b + t_{n - 2} a^{n - 2} b^2 + ... + t_1 ab^{n - 1} + b^n})
, где
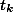
- целые числа, зависящие от n и k, но не зависящие от a и b, и при этом
})
При a=b=1 имеем:
Воспользуемся неравенством Коши о среднем арифметическом и среднем геометрическом: для любых положительных чисел x и y справедливо неравенство
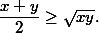
Учитывая эти неравенства, симметрию коэффициентов (*) и равенство (**), получим требуемое.
- Ответ