Решение
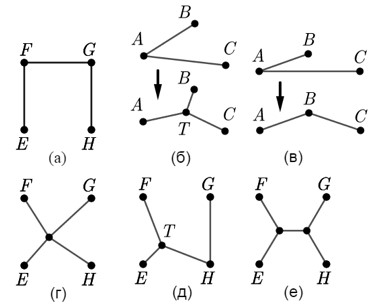
Предположим, что у нашей системы дорог перекрестков нет, то есть имеется одна дорога, соединяющая последовательно вершины квадрата E,F,G и H. Тогда ее длина будет не меньше трех сторон квадрата (буквы «П» на рис. (а)), то есть не меньше 12 (дорога, соединяющая соседние вершины квадрата, не меньше его стороны).
Значит, искомая (а в идеале кратчайшая) система дорог должна иметь перекрестки (например, как на рис. (д)). Чтобы понять, каким образом можно эффективно общую длину дорог уменьшать, полезно прежде обратить внимание на некоторые свойства, которыми кратчайшая система дорог обязана обладать:
I. Кратчайшая система дорог состоит из отрезков, соединяющих перекрестки и вершины квадрата. Это очевидно, поскольку кратчайшим путем из одной точки в другую является отрезок прямой. Отметим без доказательства, хотя и это почти очевидно, что для любой системы городов кратчайшая система дорог их соединяющая – это связный граф без замкнутых путей, ребрами которого служат отрезки.
II. Каждый перекресток должен быть соединен минимум с тремя вершинами графа (вершинами квадрата или перекрестками). (Если он соединен только с двумя, то смысла в нем немного: его можно удалить, а эти две вершины соединить напрямую; получится короче.)
III. Угол между любыми двумя дорогами, выходящими из одного перекрестка (или из одной вершины квадрата) не может быть меньше
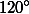
. Действительно, пусть из точки A выходят дороги AB и AC, и угол BAC меньше
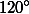
. Тогда дороги AB и AC можно заменить дорогами с меньшей суммарной длиной. Если в треугольнике ABC все внутренние углы меньше
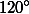
, то дороги AB и AC заменим на дороги TA, TB и TC, где T – точка Торичелли треугольника ABC (рис. (б)). Если же, например, угол B больше
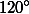
, то AB и AC заменим на AB и BC (рис. (в)).
IV. Из одного перекрестка выходят ровно три дороги под углами
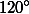
(иначе длина дорог может быть уменьшена). Это немедленно следует из свойств (II) и (III).
Предположим, что система дорог обладает одним перекрестком. Если он соединен со всеми вершинами (рис. (г)), то длина дорог не меньше суммы диагоналей, которая равна
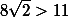
. Если же он соединен только с тремя вершинами (рис. (д)), то T – точка Торичелли треугольника EFH, вершина G соединена с F. В этом случае длина дорог приблизительно равна 11,7. Более того, нарушено свойство (III), так как
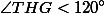
, а значит, длину дорог можно уменьшить, добавив еще один перекресток (как в случае на рис. (б)).
Пусть перекрестков два. Из соображений симметрии расположим их на параллельной двум сторонам оси симметрии квадрата (рис. (е)) так, чтобы из каждого перекрестка дороги выходили под углами
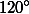
(свойство (IV)). В этом случае суммарная длина дорог равна
 < 10,92. })
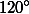 . Сумма расстояний AT+BT+CT от точки T до вершин треугольника минимальна, если из точки T стороны треугольника видны под углом
. Сумма расстояний AT+BT+CT от точки T до вершин треугольника минимальна, если из точки T стороны треугольника видны под углом 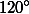 ( T – точка Торичелли треугольника). Если же один из углов треугольника больше или равен
( T – точка Торичелли треугольника). Если же один из углов треугольника больше или равен 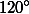 , то точкой минимума суммы расстояний будет вершина этого угла.
, то точкой минимума суммы расстояний будет вершина этого угла.