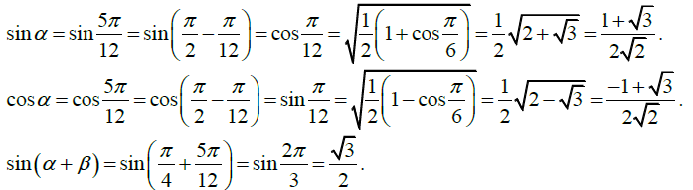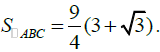10-6-12
Из точки A, лежащей на окружности радиуса 3, проведены
хорды AB, AC и касательная AD. Угол между хордами равен π/4, а угол
между хордой AC и касательной AD, который не содержит хорды AB,
равен 5π/12. Вычислите целую площади треугольника ABC .
- Решение
Решение
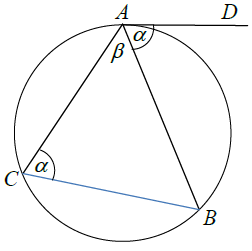
Пусть <DAC = a , <BAC = β , а радиус окружности равен R .
Известно, что <ACB = <DAC = a.
По теореме синусов |AB|/sin a = |BC|/sin β = 2R.
Следовательно, |AB| = 2R sin a, |BC| = 2R sin a . Sabc = 1/2 |AB| |BC| sin(<ABC).
Следовательно, Sabc = 2R2sin a sin β sin(a + β) (2)
Для вычисления величины площади
требуется знать значения sin a и sin (a + β).
Вычислим эти величины в условиях задачи.
Для этого посчитаем sin a и cos a.
Подставив полученные значения в (2), нетрудно получить, что
Остается вычислить ответ.
- Ответ