Решение
Рассмотрим случай, когда угол 
треугольника 
острый (случаи
тупого и прямого углов рассматриваются аналогично).
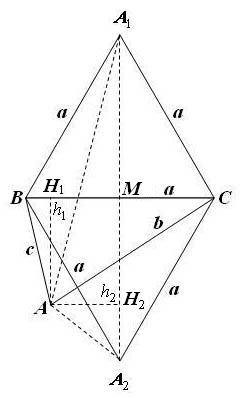
По условию треугольники
и
- правильные, значит
прямая
перпендикулярна
, более того
, где
- одновременно являются
высотами, медианами и биссектрисами треугольников
и
соответственно. Поэтому
и
.
Обозначим высоты
и
треугольников
и
,
опущенные на стороны
и
, соответственно
и
.
Рассмотрим прямоугольник
. В нем
,
. Следовательно, из треугольника
:
, а
(модуль снимается в
зависимости от знака указанной разности, хотя в данной задаче это не
играет роли).
Аналогично,
и
.
Применяя теорему Пифагора к прямоугольным треугольникам
,
,
,
, получим:
Складывая два последних равенства, получим
Подставим полученные выражения для
и
в искомую сумму
квадратов и с учетом выражения для
преобразуем ее: