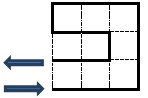
"Теплый пол"
На плоскости изображён квадрат nxn клеток. Вершины клеток будем называть узлами. Требуется в этом квадрате уложить трубу (“тёплый пол”) так, чтобы вход был в левом нижнем углу, а выход – в соседнем узле, и при этом труба прошла бы ровно один раз через каждый узел. Трубу разрешается укладывать только по границам клеток. На рисунке изображён пример укладки трубы в квадрате 3x3. Докажите, что уложить трубу возможно при любом нечётном значении n и невозможно ни при каком чётном n.