Система с единственным решением
При каких значениях параметра a система уравнений
имеет единственное решение?
- Подсказка
- Решение
- Ответ
Подсказка
1. Установить, что первое уравнение системы задаёт отрезок, а второе - окружность.
2. Единственное решение системы возможно в двух случаях:
- когда прямая, на которой лежит отрезок, касается окружности, и при этом точка касания принадлежит отрезку;
- когда окружность пересекает отрезок ровно в одной точке.
Решение
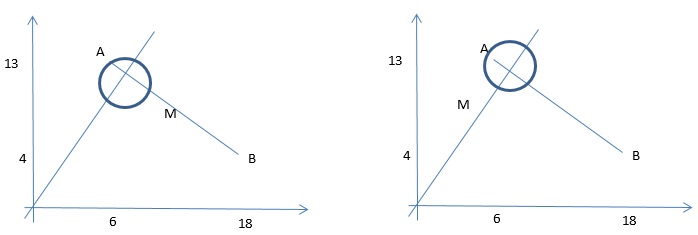
Первое уравнение системы задает ГМТ точек M(x,y) на плоскости, сумма расстояний от которых до точек A(6,13) и B(18,4) равна 15. Заметим, что 
. Поэтому, согласно неравенству треугольника, ГМТ таких точек M(x,y) суть точки отрезка AB. Второе уравнение есть уравнение окружности с центром в точке S(2a,4a) радиуса 1/2. Единственность решения системы возможна в том и только в том случае, когда окружность пересекает отрезок AB ровно в одной точке. Очевидно, что гарантированно единственная точка пересечения будет в случае касания окружности отрезком. Это произойдет тогда, когда расстояние от точки S(2a,4a) до прямой, содержащей отрезок AB, будет равно радиусу окружности, и точка касания будет попадать в отрезок AB. Уравнение прямой, содержащей AB, как нетрудно установить, имеет вид 3x+4y-70=0. Согласно формуле расстояния от точки до прямой (один из вариантов решения):
Отсюда получим два возможных значения параметра a:
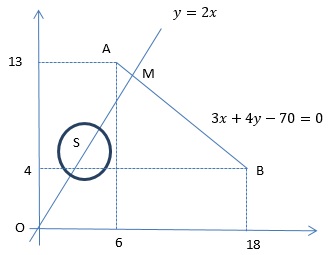
Центр окружности лежит на прямой y=2x. Точка })
пересечения прямых y=2x и 3x+4y-70=0 лежит на отрезке AB. Угол OMB острый, поэтому точка касания прямой 3x+4y-70=0 и окружности, центр которой лежит под отрезком AB, заведомо на отрезок AB попадет. Это происходит при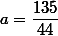 
. Если же центр S окружности лежит выше отрезка AB (это происходит при 
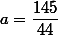), то требуются дополнительные рассуждения. Точка касания H есть проекция точки })
на прямую, содержащую отрезок AB. H попадет в отрезок AM, если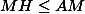 
. Имеем:
Следовательно MH < AM, и точка касания H лежит на отрезке AB. В то же время, поскольку AM < 1/2, постольку единственность решения возможна, когда окружность пересекает отрезок AB, но при этом точка A попадает вовнутрь круга. Так будет происходить с момента пересечения окружности и отрезка в точке A до момента повторного пересечения в той же точке A (не включая данные моменты).
