Иррациональные синус и косинус
Известно, что для любого натурального числа n верна формула:
Здесь 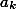 – целые числа, и
– целые числа, и 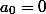 при нечётном n. Докажите, что при n≥4 числа
при нечётном n. Докажите, что при n≥4 числа
- Подсказка
- Решение
- Ответ
Подсказка
1. Использовать теорему: если многочлен с целыми коэффициентами имеет рациональный корень, то числитель дроби является делителем свободного члена, а знаменатель – делителем старшего коэффициента этого многочлена.
2. Если доказать, что косинусы иррациональны, то для соответствующих синусов иррациональность доказывается просто.
3. Иррациональность числа  }) доказать методом от противного, разбив доказательство на несколько случаев (в зависимости от кратности числа n).
доказать методом от противного, разбив доказательство на несколько случаев (в зависимости от кратности числа n).
Решение
При доказательстве будем пользоваться следующим утверждением: если рациональное число 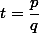 (p и q – взаимно простые целые числа) является корнем многочлена
(p и q – взаимно простые целые числа) является корнем многочлена  = a_k x^k + a_{k - 1} x^{k - 1} + ... + a_1 x + a_0 }) с целыми коэффициентами (
с целыми коэффициентами (  ), то p является делителем
), то p является делителем 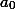 , а q – делителем
, а q – делителем 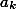 . Предположим, что
. Предположим, что }) – рациональное число (при некотором n≥4).
– рациональное число (при некотором n≥4).
1) Пусть n кратно 4, то есть n=4t, t∈N. Тогда  = \cos \left( {t\frac{\pi }{{4t}}} \right) =})
^t + a_{t - 1} \cdot \left( {\cos \frac{\pi }{n}} \right)^{t - 1} + a_{t - 2} \cdot \left( {\cos \frac{\pi }{n}} \right)^{t - 2} + ... + a_1 \cdot \left( {\cos \frac{\pi }{n}} \right) + a_0 .}) Такое равенство невозможно, так как левая часть – иррациональное число
Такое равенство невозможно, так как левая часть – иррациональное число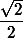 , тогда как значение правой части рационально.
, тогда как значение правой части рационально.
2) Пусть n – нечётное число и n≥5. Тогда
Тогда }) – рациональный корень многочлена
– рациональный корень многочлена  , и, по сформулированному выше утверждению,
, и, по сформулированному выше утверждению,  = \frac{1}{{2{}^m}}}) , где
, где 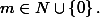 Но это невозможно, так как при n≥5 выполняется неравенство
Но это невозможно, так как при n≥5 выполняется неравенство  > \cos \left( {\frac{\pi }{3}} \right) = \frac{1}{2} \ge \frac{1}{{2{}^m}} }) . Вновь получено противоречие.
. Вновь получено противоречие.
3) Пусть, наконец, n чётно и не кратно 4. Тогда n имеет нечётный делитель p, то есть n=pt, p – нечетное число; более того, если n∉{2,6}, то всегда можно выбрать p так, что p≥5. Тогда
Таким образом, для всех натуральных n≥4 показано, что }) – иррациональное число.
– иррациональное число.
Покажем, что для всех натуральных n≥4, n≠6 число  }) иррационально. Предположим, что при некотором n
иррационально. Предположим, что при некотором n  }) – рациональное число.
– рациональное число.
1) Пусть n – чётное число, n=2k,k≥4. Тогда 
}) . По доказанному, число
. По доказанному, число 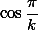 иррационально, следовательно иррационально и число
иррационально, следовательно иррационально и число  }) .
.