Выполним преобразования
По условию
})
. Следовательно, числа
лежат на интервале
})
. Рассмотрим функцию
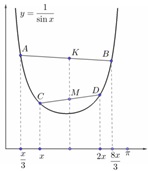
 = \frac{1}{{\sin x}} })
. Ее вторая производная
 = \frac{{2\cos ^2 x}}{{\sin ^3 x}} + \frac{1}{{\sin x}}
})
положительна для всех
})
, значит, на этом интервале функция выпукла вниз. На координатной плоскости отметим точки
} \right),\;B\left( {\frac{{8x}}{3},\;f\left( {\frac{{8x}}{3}} \right)} \right),\;C\left( {x,\;f\left( x \right)} \right) })
и
} \right). })
Левая часть последнего неравенства – сумма ординат точек A и B или, что то же самое, – удвоенная ордината точки K – середины отрезка AB. Аналогично, правая часть последнего неравенства – удвоенная ордината точки M – середины CD. Поскольку f(x) выпукла вниз, весь отрезок AB расположен «выше» отрезка CD, а значит, ордината точки K больше ординаты точки M. Неравенство доказано.
