Решение
Таблицу размерами n×n будем обозначать
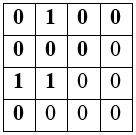
. Очевидно, что для таблицы
искомое максимальное k равно 3. Экспериментируя с таблицей
, можно заметить, что k=4 (ниже мы докажем это строго). Сделанные наблюдения позволяют предположить, что для произвольного n>1 максимальное значение k равно n+1. Докажем это. Прежде всего, покажем, что n+2 единицы таблица содержать не может. Для этого приведем контрпример, но сначала вспомним определение трансверсали.
Трансверсалью таблицы
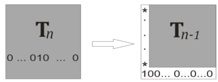
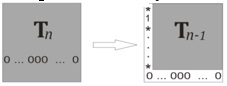
называют набор из n ячеек, содержащих 1, любые две из которых расположены в разных строках и разных столбцах. Ясно, что если какие-то ячейки образовывали трансверсаль, то и после перестановки строк или столбцов они снова образуют трансверсаль. На рисунке изображена таблица n×n с n+2 единицами, расположенными на главной диагонали, а также в таблице 2×2 в левом верхнем углу. Такая таблица содержит две трансверсали.
В то же время таблица, у которой все 1 лежат на или выше побочной диагонали, содержит не более одной трансверсали. Значит, к требуемому в задаче виду таблица на рисунке приведена быть не может. Поэтому k≤n+1.
Покажем, что n+1 единицу всегда можно перенести на побочную диагональ или выше. Итак, дана таблица
, содержащая
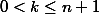
единиц. В такой таблице обязательно есть строка или ровно с одной 1, или не содержащей единиц вовсе. Рассмотрим эти случаи.
1) В таблице
есть строка, содержащая ровно одну 1. Поставим эту строку на последнее место. Затем, переставляя столбцы, переместим эту единственную 1 в крайний левый столбец.
- 2) В таблице есть строка, содержащая только нули. Поставим эту строку на последнее место. Переставляя столбцы, сделаем так, чтоб в крайнем левом столбце была хоть одна единица.
В каждом случае получена подтаблица
, содержащая, по крайней мере, на одну 1 меньше, чем таблица
. С таблицей
можно выполнить аналогичные преобразования. В результате за n-2 шага придем к таблице
, для которой уже установлено, что k=3. Формула k=n+1 доказана.
