Решение
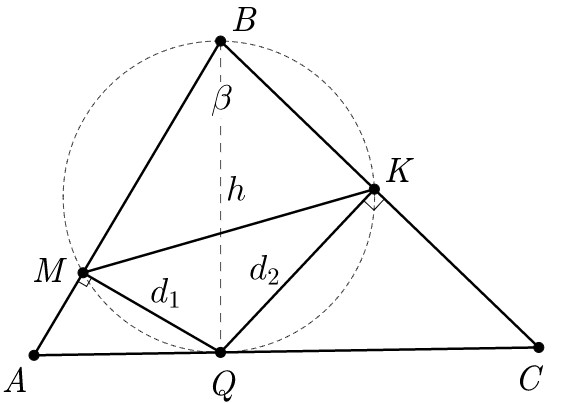
Длины перпендикуляров, опущенных из точки Q основания AC, обозначим как d1 и d2; пусть ∠B=β. Четырехугольник MBKQ вписан в окружность, и BQ ее диаметр. По формуле для радиуса описанной около треугольника MBK окружности имеем:
Поскольку величина угла β фиксирована, длина отрезка MK тем меньше, чем меньше длина BQ. Значит, точка Q – это основание перпендикуляра, опущенного из точки B на AC, и BQ – высота (основание перпендикуляра Q лежит именно на стороне AC, а не на ее продолжении, так как углы A и C острые; если бы, скажем, угол A был тупым, то точка M оказалась бы на продолжении стороны AB, а не на ней самой); положим BQ=h. Найдем площадь ∆ABQ, считая пока h известной величиной. Имеем
Тогда

Аналогично,

. Искомая площадь равна их сумме:
Остается найти h. Так как h=BQ, то из (1) следует, что

Найдем MK из ∆MQK (в нем

) по теореме косинусов:
Итак,
Чтобы воспользоваться (2), прежде для удобства вычислим:
Аналогично,
^2 }}{{\sin ^2 \beta }}. })
Подставив полученные выражения в (2), находим:
Используя теперь числовые данные задачи, получаем ответ.