Решение
Докажем вспомогательное утверждение.
Утверждение. Пусть пара натуральных чисел
})
удовлетворяет исходному уравнению
Тогда
1)
2) уравнение (1) имеет еще одно решение в натуральных числах
.})
: 1) Положив
и подставив в (1), получим
Очевидно, что
2) По условию, число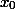
является корнем многочлена
 = x^2 - 6y_0 x + y_0^2 + 1.\quad \quad \quad (2)})
По теореме Виета, этот многочлен еще имеет корень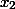
, причем
Отсюда следует, что
и
Утверждение доказано.
Предположим, что какое-то решение
уравнения (1) найдено. Без ограничения общности можно считать, что в этой паре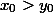
(неравенство строгое в силу пункта 1 утверждения). Будем это записывать как
 = x_0 .})
Согласно утверждению, уравнение (1) еще имеет решение
Это означает, что для многочлена (2) справедливы равенства
 = \psi \left( {6x_0 - y_0 } \right) = 0.})
Заметим, что
 = y_0^2 - 6y_0^2 + y_0^2 + 1 < 0.})
Поэтому число
лежит между корнями многочлена (2), а именно:
Следовательно,
 = y_0 < \max \left( {x_0 ,\;y_0 } \right).})
Итак, для любого решения
существует другое решение, у которого максимальный элемент окажется меньше. Таким образом, мы можем строить новые решения, у которых максимальный элемент становится все меньше. Но при этом этот максимальный элемент, постоянно уменьшаясь, остается натуральным числом, что невозможно. Пришли к противоречию. Значит, исходное уравнение (1) решений в натуральных числах не имеет.