Решение
Заметим, что
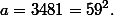
Тогда
\; \Leftrightarrow \;(b - 59)(b + 59) = 0\;(\bmod \;N)\; })
. Следовательно, пары чисел (b-59) и N или (b+59) и N имеют общие делители, отличные от 1. Найдём наибольший общий делитель чисел (b+59) и N по алгоритму Евклида.
26069=6∙4179+995,
4179=4∙995+199,
Следовательно, НОД((b+59),N)=199 – простое число. Остаётся разделить N на 199 и убедиться, что частное - также простое число.
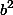 на N равен a. Найдите разложение числа N на простые множители.
на N равен a. Найдите разложение числа N на простые множители.