Площадь части сферы
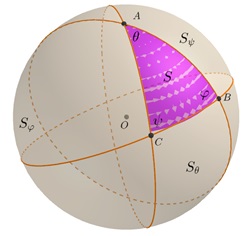
Из центра O сферы радиуса R проведены три луча, пересекающие сферу в точках A, B и C. Известно, что ∠AOB=∠AOC=∠BOC=60°. Найдите площадь части сферы, ограниченной плоскостями (AOB), (AOC) и (BOC).- Подсказка
- Решение
- Ответ
Подсказка
1) Применить (получить) формулу для площади S криволинейного △ABC с углами φ, ψ, θ:
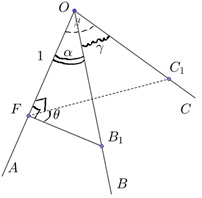
2) Для трехгранного угла OABC выразить его двугранные углы φ, ψ, θ через плоские углы α, β, γ (применить теорему косинусов для трехгранного угла).
Решение
В задаче речь идет о трехгранном угле с вершиной в центре сферы, высекающем на сфере криволинейный треугольник. Площадь этого треугольника требуется выразить через радиус сферы и данные в условии плоские углы трехгранного угла, которые будем обозначать ∠AOB=α, ∠AOC=β, ∠BOC=γ.
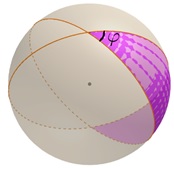
Рассмотрим сначала две различные плоскости, проходящие через центр сферы. Пусть угол между этими плоскостями равен φ. Плоскости пересекают сферу по большим окружностям. Касательные к окружностям в их точке пересечения также образуют угол φ. Площадь поверхности сферы равна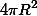 
. Площадь высекаемой плоскостями «дольки» (указанной на рисунке цветом) очевидно пропорциональна величине φ и равна 
.
Три плоскости (содержащие грани трехгранного угла) разбивают сферу на 8 треугольников. Искомую площадь криволинейного треугольника ABC обозначим через S, а его углы (которые, очевидно, являются двугранными углами трехгранного угла OABC) за φ, ψ, θ. Площади криволинейных треугольников, примыкающих к сторонам треугольника ABC, обозначим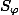 
, 
, 
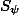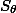. С каждым из этих треугольников △ABC образует «дольку», поэтому 
, 
, 
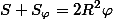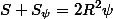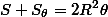. Оставшиеся из 4-х нерассмотренных криволинейных треугольников симметричны 4-м рассмотренным относительно центра сферы. Значит, суммарная площадь рассматриваемых четырех треугольников равна половине площади сферы, то есть 
. Отсюда после несложных преобразований для площади S криволинейного △ABC с углами φ, ψ, θ получим известную формулу
Остается для трехгранного угла OABC выразить его двугранные углы φ, ψ, θ через данные в задаче плоские углы α, β, γ. Для этого применим известную теорему косинусов для трехгранного угла.
Теорема. Дан трехгранный угол OABC, в котором ∠AOB=α, ∠AOC=β, ∠BOC=γ. Пусть θ – величина двугранного угла при ребре AO. Тогда
По условию, все плоские углы одинаковы α=β=γ=60°. Поэтому все двугранные углы φ, ψ, θ также равны между собой. Согласно (2), 
и 
. Подставляя найденные значения в формулу (1), получаем  \cdot R^2 })
.