7.11.2005

Найти все значения параметра ${a}$ , при которых уравнение

${ 2\cdot|x+3|-3\cdot|x+4|+3\cdot|x+5|=ax }$

имеет ровно два различных решения.

Подсказка

Решение

Решение

Раскроем модули методом интервалов:

${ \left[\begin{array}{l} \left\{\begin{array}{l} x\le-5,\\ -2(x+3)+3(x+4)-3(x+5)=ax, \end{array}\right.\\ \left\{\begin{array}{l} -5<x\le-4,\\ -2(x+3)+3(x+4)+3(x+5)=ax, \end{array}\right.\\ \left\{\begin{array}{l} -4<x\le-3,\\ -2(x+3)-3(x+4)+3(x+5)=ax, \end{array}\right.\\ \left\{\begin{array}{l} x>-3,\\ 2(x+3)-3(x+4)+3(x+5)=ax. \end{array}\right. \end{array}\right. }$

Рассмотрим 4 случая.
1) ${x\le-5}$ . Тогда уравнение примет вид ${(a+2)x=-9}$ . Если ${a=-2}$ , то решений нет. Если ${a\ne-2}$ , то ${x_1=-9/(a+2)}$ . Это решение должно удовлетворять условию ${x\le-5}$ . Выясним, при каких ${a}$ это так:

${ \frac{-9}{a+2}\le-5 \quad\Leftrightarrow\quad \frac{9}{a+2}\ge5 \quad\Leftrightarrow\quad \frac{-5a-1}{a+2}\ge0 \quad\Leftrightarrow\quad -2<a\le-\frac15. }$

Таким образом, при ${-2<a\le-1/5}$ существует одно решение ${x_1}$ , принадлежащее множеству ${(-\infty,-5]}$ .
2) ${-5<x\le-4}$ . Тогда уравнение примет вид ${(a-4)x=21}$ . Если ${a=4}$ , то решений нет. Если ${a\ne4}$ , то ${x_2=21/(a-4)}$ . Это решение должно удовлетворять условию ${-5<x\le-4}$ . Выясним, при каких ${a}$ это так:

${ -5<\frac{21}{a-4}\le-4 \quad\Leftrightarrow\quad \left\{\begin{array}{l} \frac{5a+1}{a-4}>0,\\ \frac{4a+5}{a-4}\le0, \end{array}\right. \quad\Leftrightarrow\quad \left\{\begin{array}{l} \left[\begin{array}{l} a>4,\\ a<-1/5, \end{array}\right.\\ -5/4\le a<4, \end{array}\right. }$

то есть ${-5/4\le a<-1/5}$ . Таким образом, при указанных ${a}$ существует одно решение ${x_2}$ , принадлежащее множеству ${(-5,-4]}$ .
3) ${-4<x\le-3}$ . Тогда уравнение примет вид ${(a+2)x=-3}$ . Если ${a=-2}$ , то решений нет. Если ${a\ne-2}$ , то ${x_3=-3/(a+2)}$ . Это решение должно удовлетворять условию ${-4<x\le-3}$ . Выясним, при каких ${a}$ это так:

${ -4<\frac{-3}{a+2}\le-3 \quad\Leftrightarrow\quad \left\{\begin{array}{l} \frac{4a+5}{a+2}>0,\\ \frac{3a+3}{a+2}\le0, \end{array}\right. \quad\Leftrightarrow\quad \left\{\begin{array}{l} \left[\begin{array}{l} a>-5/4,\\ a<-2, \end{array}\right.\\ -2<a\le-1, \end{array}\right. }$

то есть ${-5/4<a\le-1}$ . Таким образом, при указанных ${a}$ существует одно решение ${x_3}$ , принадлежащее множеству ${(-4,-3]}$ .
4) ${x>-3}$ . Тогда уравнение примет вид ${(a-2)x=9}$ . Если ${a=2}$ , то решений нет. Если ${a\ne2}$ , то ${x_4=9/(a-2)}$ . Это решение должно удовлетворять условию ${x>-3}$ . Выясним, при каких ${a}$ это так:

${ \frac{9}{a-2}>-3 \quad\Leftrightarrow\quad \frac{a+1}{a-2}>0 \quad\Leftrightarrow\quad \left[\begin{array}{l} a>2,\\ a<-1. \end{array}\right. }$

Таким образом, при ${a\in(-\infty,-1)\cup(2,\infty)}$ существует одно решение ${x_4}$ , принадлежащее множеству ${(-3,\infty)}$ .
Подведем итог. Для этого разобьем все множество вещественных значений параметра ${a}$ на промежутки, возникшие в решении. Они определяются точками ${a=-2}$ , ${-1/5}$ , ${-5/4}$ , ${-1}$ , 2, поэтому всего получается 6 промежутков. В каждом промежутке подсчитаем число решений уравнения, используя полученные в пп. 1)-4) результаты.

7.11.2005.jpg

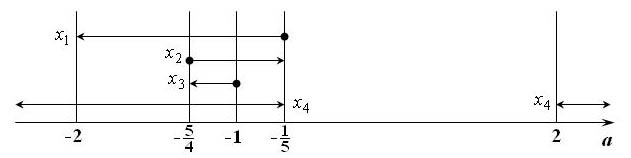
     В итоге:
      ${a\in(-\infty;-2) \quad \Rightarrow \quad }$ решение одно ${ \{x_1\};}$
      ${a=-2 \quad \Rightarrow \quad }$ решение одно ${\{x_4\};}$
      ${a\in(-2;-\frac{5}{4})\quad \Rightarrow \quad}$ решений два ${\{x_1, x_4\};}$
      ${a=-\frac{5}{4} \quad \Rightarrow \quad}$ решений три ${\{x_1,x_2,x_4\};}$
      ${a\in(-\frac{5}{4};-1)\quad \Rightarrow \quad}$ решений четыре ${\{x_1, x_2,x_3,x_4\};}$
      ${a=-1 \quad \Rightarrow \quad}$ решений три ${\{x_1,x_2,x_3\};}$
      ${a\in(-1;-\frac{1}{5})\quad \Rightarrow \quad}$ решений два ${\{x_1, x_2\};}$
      ${a=-\frac{1}{5} \quad \Rightarrow \quad}$ решение одно ${\{x_1\};}$
      ${a\in(-\frac{1}{5};2)\quad \Rightarrow \quad}$ решений нет;
      ${a=2 \quad \Rightarrow \quad}$ решений нет;
      ${a\in(2;+\infty) \quad \Rightarrow \quad}$ решение одно ${\{x_4\};}$
      В результате получим, что два решения уравнение имеет при ${a\in(-2,-5/4)\cup(-1,-1/5)}$ .
     Примечание: существует другое решение задачи, основанное на построении графика функции ${y=2\cdot|x+3|-3\cdot|x+4|+3\cdot|x+5|}$ и на исследовании расположения прямой ${y=ax}$ относительно первого графика.

Ответ

7.11.2005

Подсказка

Решение

Ответ