Решение
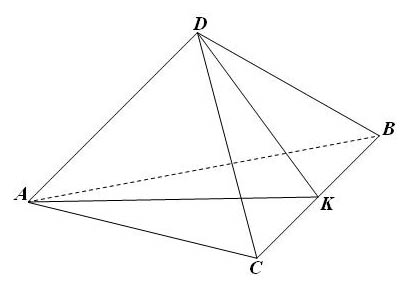
1. Рассмотрим скрещивающиеся ребра тетраэдра

и

Пусть

- середина ребра

Тогда прямые

и

перпендикулярны ребру

(поскольку они являются одновременно медианами, биссектрисами и высотами в равносторонних треугольниках). Значит, прямая

перпендикулярна плоскости

Окончательно получаем, что ребра тетраэдра

и

перпендикулярны.
2. Поместим тетраэдр в коробку так, чтобы его ребра

и

были параллельны ребрам основания коробки. Это можно сделать, так как:
- выше доказано, что

и

перпендикулярны,
- длина этих ребер (12 см) меньше длин основания коробки (13 и 15 см).
3. Осталось проверить, что расстояние между

и

меньше высоты коробки (9 см). Нетрудно заметить, что расстояние между

и

равно высоте треугольника

Данный треугольник является равнобедренным с основанием

и боковыми сторонами

Отрезки

и

являются высотами равностороннего треугольника со стороной 12, откуда
Теперь расстояние

между ребрами

и

вычисляем как длину высоты в треугольнике

4. Поскольку

то тетраэдр можно уместить в коробку.
