Решение
Покажем, что

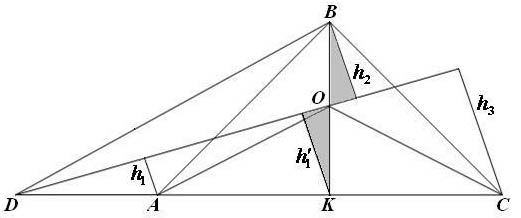
Для этого (поскольку треугольники имеют общую сторону

, см. рис) достаточно показать, что длины перпендикуляров, опущенных на

из вершин указанных треугольников, удовлетворяют равенству
Действительно, используя свойство средней линии трапеции

и

, что следует из подобия треугольников, отмеченных на рисунке серым, и соотношения 2:1 отрезков медианы, полученных точкой пересечения всех медиан треугольника, приходим к равенству (**) . А поскольку

и

(последнее равенство справедливо из-за подобия треугольников

и

, что позволяет сделать вывод о том, что высота треугольника

втрое больше высоты треугольника

), то

. Окончательно из равенства (*) получаем

