Архив задач

3.10.2011

Решите уравнение {\frac{\sin^2 3x}{\sin^2 x} = 8\cos 4x + \frac{\cos ^2 3x}{\cos ^2 x}.}

  • Подсказка

    • Подсказка

    Сгруппировать две дроби, приведя их к общему знаменателю и используя формулы сокращенного умножения и формулы синуса суммы и разности двух углов.
  • Решение

    • Решение

    Определим сначала ОДЗ данного уравнения: {\sin x\neq0,} {\cos x\neq0.} Т.е. {x\neq\frac{\pi k}{2}, k\in \mathbb {Z}.}
         Перенесем дробь из правой части уравнения в левую и приведем обе дроби к общему знаменателю:
    {\frac{\sin ^2 3x \cos^2 x - \sin^2 x \cos^2 3x}{\sin^2 x \cos^2 x}=}

    {= 8\cos 4x}
         
    Воспользуемся в числителе формулами сокращенного умножения и формулами синуса суммы и разности двух углов:
    {\sin ^2 3x \cos^2 x - \sin^2 x \cos^2 3x \cos x-\sin x \cos 3x)(\sin 3x \cos x+\sin x \cos 3x)=\sin 2x \sin 4x;}

         
    {\sin^2 x \cos^2 \sin^2 2x.}

         В итоге, исходное уравнение преобразуется к виду {\frac{\sin 2x \sin 4x}{\frac{1}{4}\sin^2 2x} = 8\cos 4x,} откуда получим {\frac{8\sin ^2 2x \cos 2x}{\sin^2 2x} = 8\cos 4x.}
         C учетом ОДЗ последнее уравнение примет вид {\cos 4x,} или, используя формулу разности косинусов, {-2\sin 3x \sin x=0.}
         В итоге получим совокупность двух уравнений:
    {\sin x=0} или {\sin 3x=0}
         Решая первое уравнение совокупности, получим {x=\frac{\pi n}{3},n\in \mathbb{Z},} но (с учетом ОДЗ) {n\neq 3k, k\in \mathbb{Z}} , значит, из полученного множества точек отбрасываем те, что на рисунке отмечены крестиком. Точки {x = \pm \frac{\pi }{3} + \pi m, m\in \mathbb{Z},} соединенные пунктирными линиями на рисунке, являются решениями исходного уравнения. Точки, помеченные кружочками, определяют исключения (т.е. эти точки не входят в ОДЗ).
    3.10.2011.jpg
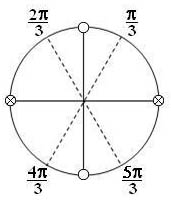
    Корни второго уравнения {\sin x=0} совокупности не удовлетворяют условиям ОДЗ.
  • Ответ

    • Ответ

    {x = \pm \frac{\pi }{3} + \pi m, m\in \mathbb{Z}.}